Dynamic Nuclear Self-Polarization Induced by Circularly Polarized Light
Nuclear magnetic moment, one of the important parameters that help in understanding the structure of nuclei, is often measured using NMR techniques. However, in this case, the nuclei under study require to be polarized. While various methods of nuclear polarization have been developed, there is no versatile method available. In order to carry out systematic studies on the nuclear structures of short-lived neutron-rich isotopes such as In, we are developing a method for nuclear polarization by applying a technique called dynamic nuclear self-polarization (DYNASP).
DYNASP was theoretically predicted by Dyakonov et al. This phenomenon is observed in type III-V semiconductors when electrons are excited to the conduction band by linearly polarized light. The lattice nuclei are self-polarized through the contact hyperfine interaction between the electrons and the lattice nuclei. A large nuclear polarization suddenly occurs below the critical temperature (Tc). We have generalized the DYNASP theory by taking into account the conduction electrons polarized by circularly polarized light. We have found that circularly polarized light enhances nuclear polarization, thus increasing the sensitivity of the NMR measurements. Fig.1 shows the temperature dependence of the nuclear polarization. When the conduction electrons are not polarized (α=0), a large nuclear polarization is observed only at temperatures below Tc, and the polarization vanishes above Tc. When the conduction electrons are polarized (|α|>0), nuclear polarization occurs even above Tc. Another interesting feature of DYNASP has been revealed by using circularly polarized light; nuclear polarization shows a hysteresis, illustrated in Fig.2 The hysteresis enables easy control of the direction of the nuclear polarization by adopting an optical method.
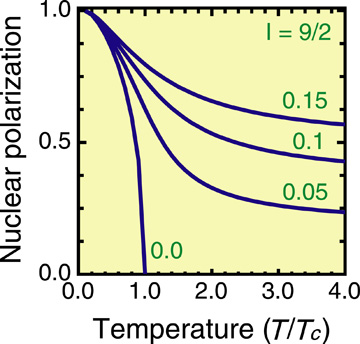
Fig. 1: Temperature dependence of nuclear polarization
The spin of the lattice nuclei is assumed to be I = 9/2. The numbers beside the curves are the values of the parameters (α) relevant to conduction-electron polarization. When |α| > 0, the lattice nuclei are polarized even at temperatures above the critical temperature (T/Tc > 1).
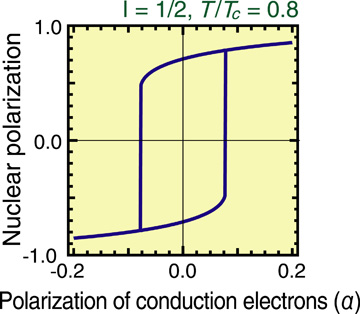
Fig. 2: Hysteresis loop of nuclear polarization.
The abscissa is the parameter α relevant to conduction-electron polarization. The spin of the lattice nuclei is assumed to be I = 1/2.
To examine the DYNASP phenomenon, we are preparing an apparatus, which is shown in Fig. 3. Once the generalized DYNASP is confirmed, we will apply the technique to magnetic moment measurements. A combination of the DYNASP technique with NMR techniques is expected to be useful in semiconductor studies and in applications such as quantum computing.
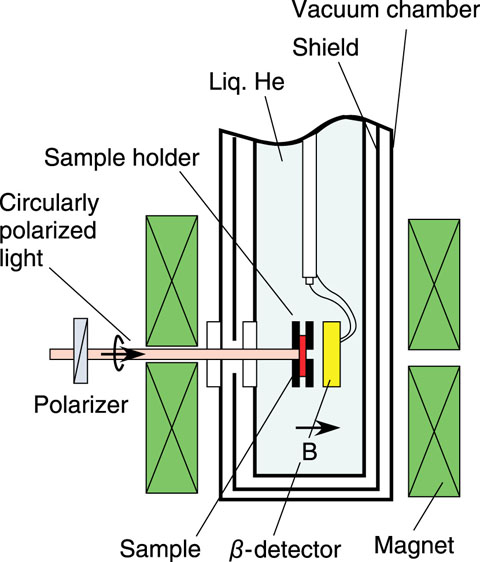
Fig. 3: Schematic experimental setup for studying DYNASP. A laser beam is injected from the left hand windows. β-rays emitted from a neutron-activated sample are measured. When the lattice nuclei of the sample are polarized, anisotropy of the β-ray emission can be seen.
Acknowledgement
This work was supported by KAKENHI
(C)(21540307).
References
The 16 IUPAP International Conference on Electromagnetic Isotope Separators and Techniques Related to Their Applications (EMIS2012), Dec. 2-7, 2012, Matsue, Japan,
M. Koizumi, J. Goto, S. Matsuki, and S. Nakamura.
“Dynamic nuclear self polarization for measurements of nuclear magnetic moments”,
"Dynamic nuclear self-polarization with circularly polarized light",
Koizumi, M. Goto, J. and Matsuki, S.,
Journal of Applied Physics, vol.110, no.1, 2011, 013911.
(This paper has selected for the issue of July 25, 2011 (vol. 24(4)) of Virtual Journal of Nanoscale Science & Technology)
JAEA R&D Review 2011, p. 80.


